Ever heard about “No Free Lunch” theorem? It’s a term familiar in machine learning. In a nutshell, it defines that no one machine learning algorithm works best for every problem. It’s especially relevant for supervised learning (i.e. predictive modeling).
For instance, you can’t say that neural networks are always better than decision trees or vice-versa. There are many factors at play, such as the size and your dataset’s structure.
For the sake of suggestion, you should try many different algorithms for your problem, while using a hold-out “test set” of data to evaluate performance and select the champion.
Indeed, the algorithms you try must be apposite for your problem, which is where choosing the right machine learning task becomes crucial. In simple terms, to clean your house, you might use a vacuum, a broom, or a mop, but you wouldn’t bust out a shovel and start digging.
The Big Principle
However, there is a universal principle that underlies all supervised machine learning algorithms for predictive modelling.
Machine learning algorithms are described as learning a target function (f) that best maps input variables (X) to an output variable (Y): Y = f(X)
This is a general learning task where we would like to make predictions in the future (Y) given new examples of input variables (X). We don’t know what the function (f) looks like or its form. If we did, we would use it directly and we would not need to learn it from data using machine learning algorithms.
The most widely used application of machine learning is to learn the mapping Y = f(X) to make predictions of Y for new X. This is called predictive modelling or predictive analytics and our objective is to make the most accurate predictions possible.
For machine learning fresher who are eager to understand the basic of machine learning, here is a walkthrough of the top 10 machine learning algorithms used by data scientists.
|
10 MACHINE LEARNING ALGORITHMS YOU SHOULD KNOW
|
Linear Regression
Linear regression is perhaps one of the most well-known and well-understood algorithms in statistics and machine learning.
Predictive modeling is primarily associated with minimizing the error of a model or making the most accurate predictions possible, at the expense of explainability.
We will borrow, reuse and steal algorithms from many different fields, including statistics and use them towards these ends.
The representation of linear regression is an equation that describes a line that best fits the relationship between the input variables (x) and the output variables (y), by finding specific weightings for the input variables called coefficients (B).
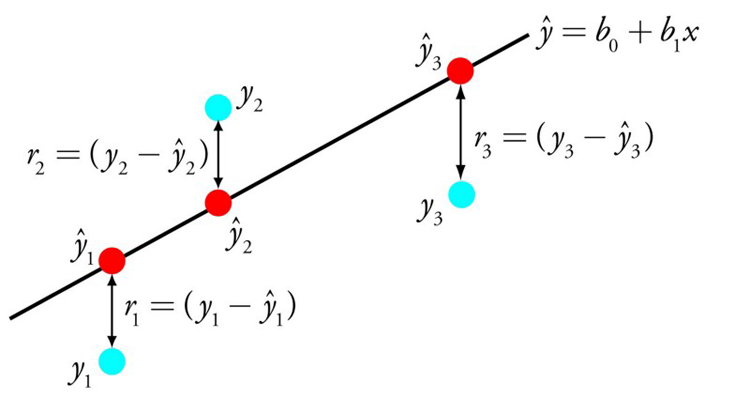
For instance: y = B0 + B1 * x
We will predict y given the input x and the goal of the linear regression learning algorithm is to find the values for the coefficients B0 and B1.
Different techniques can be used to learn the linear regression model from data, such as a linear algebra solution for ordinary least squares and gradient descent optimization.
Linear regression has been used for more than 200 years and has been extensively studied. Some good thumb rules when using this technique are to remove variables that are very similar (correlated) and to remove noise from your data, if possible. It is a fast and simple technique and good first algorithm to try.
Logistic Regression
Another technique borrowed by machine learning from the field of statistics is Logistic Regression. It is the de facto method for binary classification problems (problems with two class values).
Logistic regression is similar to linear regression in that the goal is to find the values for the coefficients that weight each input variable. Unlike linear regression, the prediction for the output is transformed using a non-linear function called the logistic function.
The logistic function looks like a big S and will transform any value into the range 0 to 1. This is useful because we can apply a rule to the output of the logistic function to snap values to 0 and 1 (e.g. IF less than 0.5 then output 1) and predict a class value.
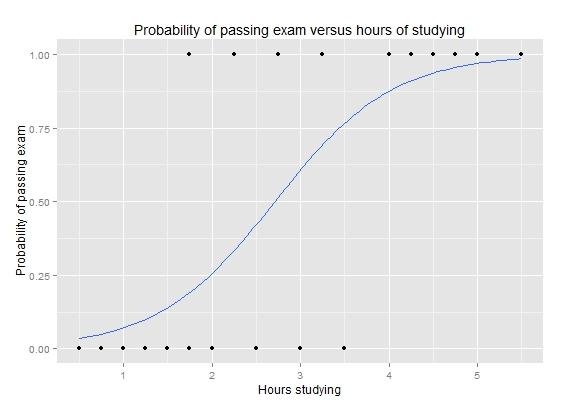
Given the way that the model is learned, the predictions made by logistic regression can also be used as the probability of a given data instance belonging to class 0 or class 1. This can be useful for problems where you need to give more rationale for a prediction.
Resembling linear regression, logistic regression does work better when you eliminate attributes that are unrelated to the output variable as well as attributes that are very similar (correlated) to each other. It’s a fast model to learn and effective on binary classification problems.
Linear Discriminant Analysis
Logistic Regression is a classification algorithm traditionally limited to only two-class classification problems. If you have more than two classes then the Linear Discriminant Analysis algorithm is the preferred linear classification technique.
The representation of LDA is straight forward. It consists of statistical properties of your data, calculated for each class. For a single input variable this includes:
|
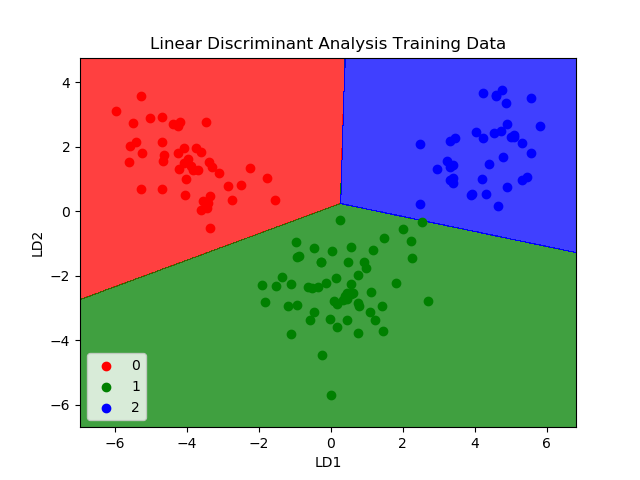
Predictions are made by calculating a discriminate value for each class and making a prediction for the class with the largest value. The technique assumes that the data has a Gaussian distribution (bell curve), so it is a good idea to remove outliers from your data beforehand. It’s a simple yet powerful method for classification predictive modelling problems.
Classification And Regression Trees
Decision Trees are a significant type of algorithm for predictive modeling machine learning with the representation of the decision tree model is a binary tree.
This is your binary tree from algorithms and data structures, nothing too fancy. Each node represents a single input variable (x) and a split point on that variable (assuming the variable is numeric).
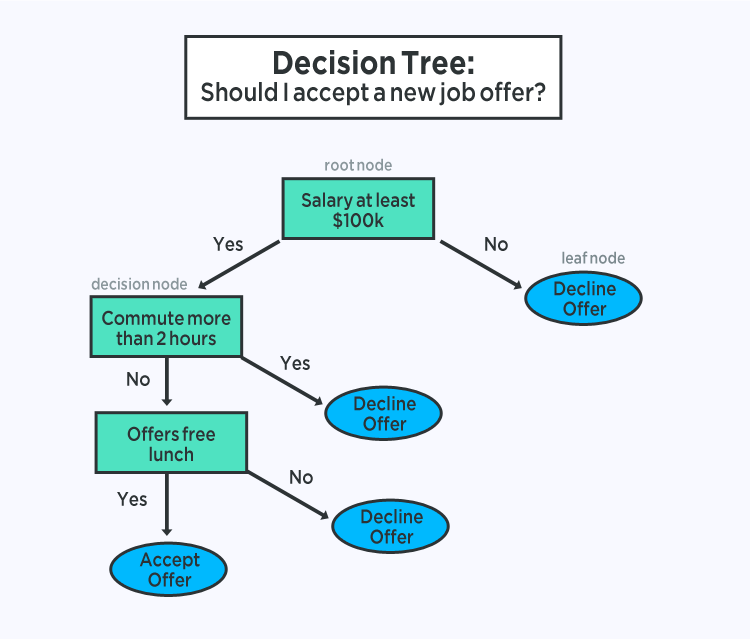
The leaf nodes of the tree contain an output variable (y) which is used to make a prediction. Predictions are made by walking the splits of the tree until arriving at a leaf node and output the class value at that leaf node.
Trees are quick to learn and very seamless for making predictions. They are also often accurate for a myriad of problems and do not require any special preparation for your data.
Naive Bayes
Naive Bayes is a simple but surprisingly powerful algorithm for predictive modelling.
The model is comprised of two types of probabilities that can be calculated directly from your training data: 1) The probability of each class; and 2) The conditional probability for each class given each x value. Once calculated, the probability model can be used to make predictions for new data using Bayes Theorem.
When your data is real-valued it is natural to assume a Gaussian distribution (bell curve) so that you can easily estimate these probabilities.
Naive Bayes is called naive because it assumes that each input variable is independent. This is a strong assumption and unrealistic for real data, nevertheless, the technique is very effective on a large range of complex problems.
K-Nearest Neighbors
The KNN algorithm is quite simple and very effective. The model representation for KNN is the entire training dataset.
Predictions are made for a new data point by searching through the entire training set for the K most similar instances (the neighbours) and summarizing the output variable for those K instances. For regression problems, this might be the mean output variable, for classification problems this might be the mode (or most common) class value.
The trick is in how to determine the similarity between the data instances. The simplest technique if your attributes are all of the same scale (all in inches for example) is to use the Euclidean distance, a number you can calculate directly based on the differences between each input variable.
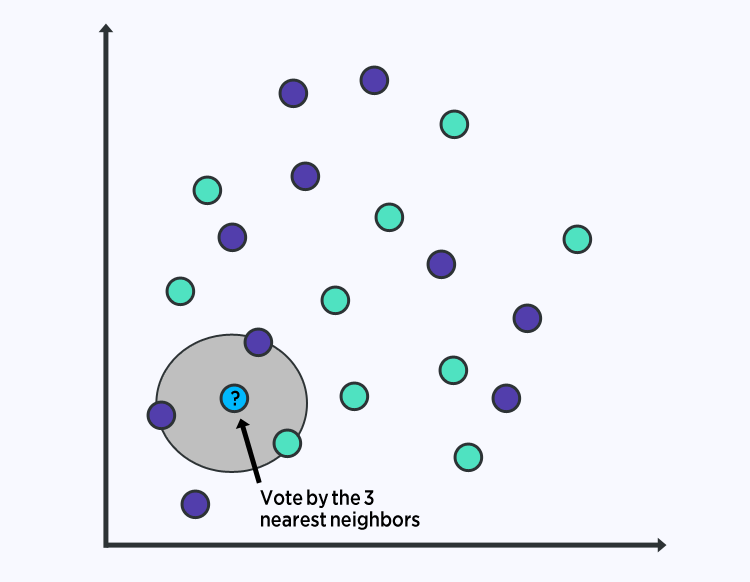
KNN may require a lot of memory or space to store all of the data, but only performs a calculation (or learn) when a prediction is needed, just in time. Moreover, you can also update and curate your training instances over time to keep predictions accurate.
The idea of distance or closeness can break down in very high dimensions (lots of input variables) which can negatively affect the performance of the algorithm on your problem. This is called the curse of dimensionality. It suggests you only use those input variables that are most relevant to predicting the output variable.
Learning Vector Quantization​
A drawback of K-Nearest Neighbors is that you need to hold on to your entire training dataset. The Learning Vector Quantization algorithm (or LVQ for short) is an artificial neural network algorithm that allows you to choose how many training instances to hang onto and learns exactly what those instances should look like.
The representation for LVQ is a collection of codebook vectors. These are selected randomly in the beginning and adapted to best summarize the training dataset over a number of iterations of the learning algorithm. After learned, the codebook vectors can be used to make predictions just like K-Nearest Neighbors. The most similar neighbor (best matching codebook vector) is found by calculating the distance between each codebook vector and the new data instance. The class value or (real value in the case of regression) for the best matching unit is then returned as the prediction. Best results can be expected if you rescale your data to have the same range, such as between 0 and 1.
If you discover that KNN gives good results on your dataset try using LVQ to reduce the memory requirements of storing the entire training dataset.
Support Vector Machines
Support Vector Machines are possibly one of the most popular and discussed machine learning algorithms.
A hyperplane is a line that splits the input variable space. In SVM, a hyperplane is selected to best separate the points in the input variable space by their class, either class 0 or class 1. In two-dimensions, you can visualize this as a line and let’s assume that all of our input points can be completely separated by this line. The SVM learning algorithm finds the coefficients that results in the best separation of the classes by the hyperplane.
The distance between the hyperplane and the closest data points is referred to as the margin. The best or optimal hyperplane that can separate the two classes is the line that has the largest margin. Only these points are relevant in defining the hyperplane and in the construction of the classifier. These points are called the support vectors. They support or define the hyperplane. In practice, an optimization algorithm is used to find the values for the coefficients that maximizes the margin.
SVM might be one of the most powerful out-of-the-box classifiers and worth trying on your dataset.
Bagging And Random Forest
Random Forest is the powerful one. It is a type of ensemble machine learning algorithm called Bootstrap Aggregation or bagging.
The bootstrap is a powerful statistical method for estimating a quantity from a data sample, say for example a mean. You take lots of samples of your data, calculate the mean, then average all of your mean values to give you a better estimation of the true mean value.
In bagging, the same approach is used, but instead for estimating entire statistical models, most commonly decision trees. Multiple samples of your training data are taken then models are constructed for each data sample. When you need to make a prediction for new data, each model makes a prediction and the predictions are averaged to give a better estimate of the true output value.
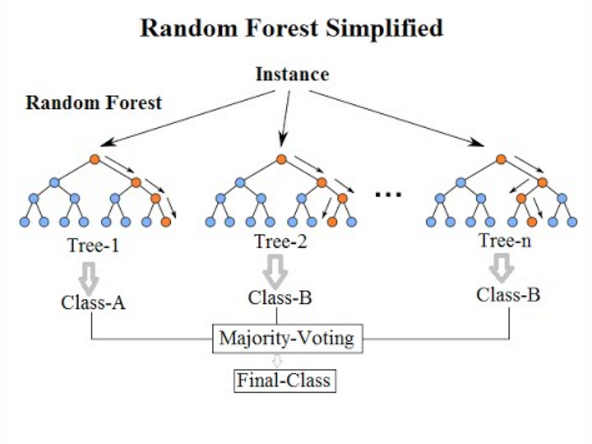
Random forest is a more like a tweak on this approach, wherein decision trees are created so that rather than selecting optimal split points, suboptimal splits are made by introducing randomness.
The models created for each sample of the data are therefore more different than they otherwise would be, but still accurate in their unique and different ways. Combining their predictions results in a better estimate of the true underlying output value.
Suppose if you get good results with an algorithm with high variance (like decision trees), you can often get better results by bagging that algorithm.
Boosting and Adaboost
Boosting is an assembly of techniques that attempts to create a strong classifier from a number of weak classifiers. This is done by building a model from the training data, then creating a second model that attempts to correct the errors from the first model. Models are added until the training set is predicted perfectly or a maximum number of models are added.
The first really successful boosting algorithm developed for binary classification was AdaBoost. It is the best start for understanding boosting. Modern boosting methods build on AdaBoost, most notably stochastic gradient boosting machines.
AdaBoost is used with short decision trees. After the first tree is created, the performance of the tree on each training instance is used to weight how much attention the next tree that is created should pay attention to each training instance. Training data that is hard to predict is given more weight, whereas easy to predict instances are given less weight. Models are created sequentially one after another, each updating the weights on the training instances that affect the learning performed by the next tree in the sequence. After all the trees are built, predictions are made for new data, and the performance of each tree is weighted by how accurate it was on training data.
A thing to note: since so much attention is put on correcting mistakes by the algorithm it is important that you have clean data with outliers removed.
Final Word of Advice
A beginner might ask when facing a wide variety of machine learning algorithms, is “which algorithm should I use?” Now the answer to these questions depends on many factors, including (1) The size, quality, and nature of data; (2) The available computational time; (3) The urgency of the task; and (4) What you want to do with the data.
Even an experienced data scientist cannot tell which algorithm will perform the best before trying different algorithms. Although there are many other Machine Learning algorithms, some popular too. However, if you’re just stepping into the world of Machine Learning, these should do the trick for you, and at the same time help you learn a good deal.
